f0 = 2000 Hz, fs = 8000Hz, B =500 Hz
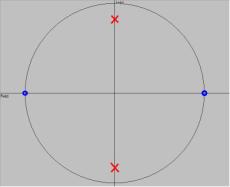
The two zeroes need to be placed at f=0 and f=Fs/2, which correspond to +1 and -1 on the unit circle in the z-domain.
In order to obtain maximum passing at the centre frequency f0, the poles must be at an angle of 2*pi*f0/Fs = pi/2. This corresponds to +/- j on the unit circle in the z-domain.
In order to find the magnitude of the poles, the equation w = 2(1-r)/r^0.5 was used. Where w = the bandwidth angle = 2*pi*500/Fs= pi/8. This resulted in a value of r = 0.82198. Therefore one pole is at j0.82198 and the other at -j0.82198.
The scaling coefficient is designed to give unity gain at the centre frequency.
This is found by evaluating H(z) with z = exp(jw), where w = pi/2. When evaluated
this gives a gain = 0.16217.
The transfer function that results is:
![]()
The corresponding pole zero plot is:
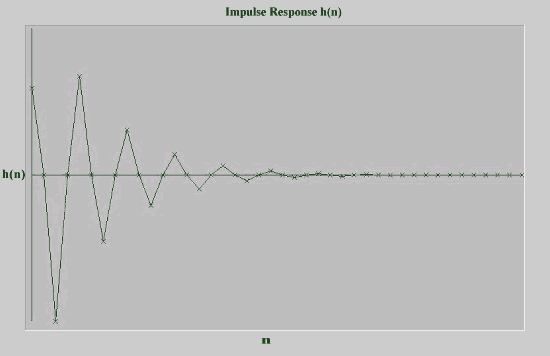
The impulse response is: