ELEC 310 formulas

complex functions

z = x + jy, f(z) = u(x,y) + jv(x,y) (1)

transfer function, ratio of polynomials with poles and zeros

$$H(z) = \frac{P(z)}{Q(z)}$$ (2)

z-transform

$$H(z) = \sum_{k=0}^{\infty} h[k]z^{-k}$$ (3)

inverse z-transform, c encloses all poles of H(z) z^k-1

$$h[k] = \frac{1}{2\pi j}\int_c H(z) z^{k-1} dz$$ (4)

c encloses all poles of H(z) z^k-1

geometric series

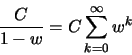$$\frac{C}{1-w} = C \sum_{k=0}^{\infty} w^k$$ (5)

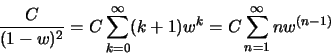$$\frac{C}{(1-w)^2} = C \sum_{k=0}^{\infty} (k+1) w^k = C \sum_{n=1}^{\infty} n w^{(n-1)}$$ (6)

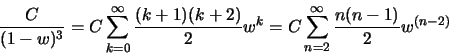$$\frac{C}{(1-w)^3} = C \sum_{k=0}^{\infty} \frac{(k+1)(k+2)}{2} w^k = C \sum_{n=2}^{\infty} \frac{n(n-1)}{2} w^{(n-2)}$$ (7)

basic inverse z-transform use geometric series with w=pz^-1 to obtain transform pair

$$H(z) = \frac{Cz}{z-p} = \frac{C}{1-pz^{-1}} \leftrightarrow h[k] = C p^k$$ (8)

Residue theorem

$$\int_c H(z) dz = 2\pi j \sum_{res} H(z)$$ (9)

sum of all residues at poles inside c.

first order pole

$$res_{z=a} F(z) = lim_{z\rightarrow a} [ (z-a)F(z) ]$$ (10)

if $F(z)=\frac{P(z)}{Q(z)}$, then

$$res_{z=a} F(z) = \frac{P(a)}{Q'(a)}$$ (11)

second order pole

$$res_{z=a} F(z) = lim_{z\rightarrow a} \frac{d}{dz}[ (z-a)^2F(z) ]$$ (12)

third order pole

$$res_{z=a} F(z) = lim_{z\rightarrow a} \frac{1}{2} \frac{d^2}{dz^2}[ (z-a)^3F(z) ]$$ (13)

mth order pole

$$res_{z=a} F(z) = lim_{z\rightarrow a} \frac{1}{m!} \frac{d^{(m-1)}}{dz^{(m-1)}}[ (z-a)^mF(z) ]$$ (14)

frequency response (amplitude and phase), sampling rate f_s

$$H(f) = H(z)\vert _{z=exp(j2\pi f/f_s)}, -f_s/2 < f < f_s/2$$ (15)

Discrete Fourier Transform (DFT) is frequency response sampled at N₀ samples around the whole unit circle -f_s/2<f<f_s/2with frequency resolution (step size) f₀=f_s/N₀

$$H(f)\vert _{f=r f_0 = r f_s/N_0}, 0 \le r \le N_0-1$$ H[r] = (16)

$$H(z)\vert _{z=exp(j2\pi f/f_s)}\vert _{f=r f_s/N_0}$$ = (17)

$$H(z)\vert _{z=exp(j2\pi r/N_0)}$$ = (18)

$$\sum_{k=0}^{N_0-1} h[k]z^{-k}\vert _{z=exp(j2\pi r/N_0)}$$ = (19)

$$\sum_{k=0}^{N_0-1} h[k]exp(-j2\pi rk/N_0)$$ = (20)

inverse DFT

$$h[k] = \frac{1}{N_0} \sum_{r=0}^{N_0-1} H[r]exp(+j2\pi rk/N_0)$$ (21)