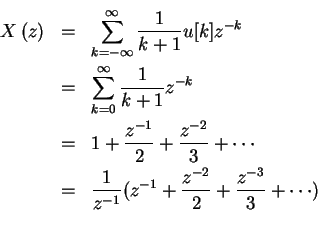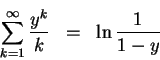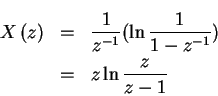Question 2

Find the z-transforms of

(a) x=[1 0 0 1]

(b) x=[1 1 1 1 ...]

(c) x=[1 2 3 4 ...]

(d) x=[1 1/2 1/3 1/4 ...]

Solution.

(a) For a sequence of numbers x[n], the z-transform is written as:

$$\begin{eqnarray*}X \left (z \right) & = & \sum_{ k= - \infty }^{ \infty } x[k]z^... ...x[2]z^{-2}+x[3]z^{-3}\\ & = & 1+0+0+z^{-3}\\ & = & 1+z^{-3} \end{eqnarray*}$$

(b) The signal x can be written as:

$$x[n] = \left \{ \begin{array}{ll} 1 & \mbox{for $n \ge 0$ }\\ 0 & \mbox{otherwise} \end {array} \right.$$

Thus

$$\begin{eqnarray*}X \left (z \right) & = & \sum_{ k= - \infty }^{ \infty } x[k]z^... ...^{-3}+....\\ & = & \frac{1}{1-z^{-1}}\\ & = & \frac{z}{z-1} \end{eqnarray*}$$

for |z|>1.

(c) When we define unit step function

$$u[n] = \left \{ \begin{array}{ll} 1 & \mbox{for $n \ge 0$ }\\ 0 & \mbox{otherwise} \end {array} \right.$$

Then the signal x is equivalent to:

$$\begin{eqnarray*}x \left [n \right] & = & u[n] + u[n-1] + u[n-2] + ... \\ & = & \sum_{ k= - \infty }^{ \infty } u[n-k] \end{eqnarray*}$$

Thus we can write

$$\begin{eqnarray*}X \left (z \right) & = & {\em z-transform}[\sum_{ k= 0 }^{ \inf... ...-k]]\\ & = & \sum_{ k= 0 }^{ \infty }{\em z-transform}[u[n-k]] \end{eqnarray*}$$

From the time-shifting property of z-transform,

$$\begin{eqnarray*}X \left (z \right) & = & \sum_{ k= 0 }^{ \infty }z^{ -k}{\em z-... ...} \frac{1}{1-z^{-1}}\\ & = & \frac{1}{\left(1-z^{-1}\right)^2} \end{eqnarray*}$$

for |z|>1.

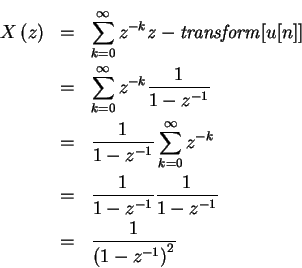
(d) The signal x is equivalent to:

$$\begin{eqnarray*}x \left [n \right] & = & \frac{1}{n+1}u[n]\\ \end{eqnarray*}$$

From the definition of the z-transform,

$$\begin{eqnarray*}X \left (z \right) & = & \sum_{ k= -\infty }^{ \infty } \frac{1... ...-1}} (z^{-1} + \frac{z^{-2}}{2} + \frac{z^{-3}}{3} + \cdots) \\ \end{eqnarray*}$$

This expression can be simplified by using the series

$$\begin{eqnarray*}\sum_{ k= 1 }^{ \infty }\frac{y^k}{k} & = & \ln \frac{1}{1-y} \end{eqnarray*}$$

Then X(z) can be expressed as

$$\begin{eqnarray*}X \left (z \right) & = & \frac{1}{z^{-1}} (\ln \frac{1}{1-z^{-1}})\\ & = & z \ln \frac{z}{z-1} \end{eqnarray*}$$