POI also calculates the frequency response H(z) with z along the unit circle
![]() for |f| less than fs/2. The sampling rate fs is not defined in Assignment 1, the POI software lets you choose the sampling rate. For
fs = 44,100 Hz, calculate the frequency response for each of the 3 filters of Assignment 1. Do this two ways:
for |f| less than fs/2. The sampling rate fs is not defined in Assignment 1, the POI software lets you choose the sampling rate. For
fs = 44,100 Hz, calculate the frequency response for each of the 3 filters of Assignment 1. Do this two ways:
1) Use the POI software to place the poles and zeros in the complex plane, and let the program calculate the frequency response.
2) Work out the algebraic expression for the frequency response and plot using Matlab.
Compare the results from POI and Matlab.
Solution.
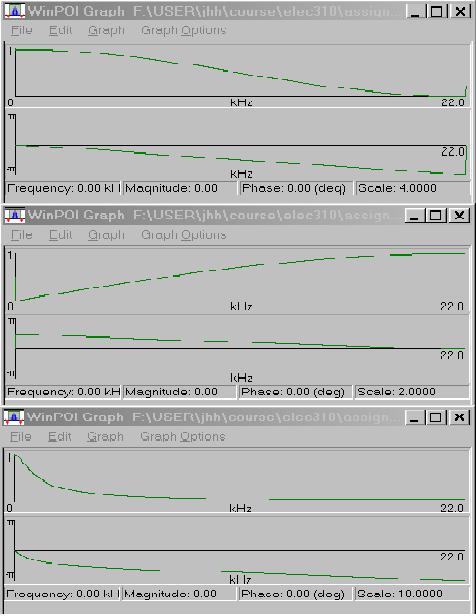
1) Results from POI software
Frequency responses calculated from POI software are shown in Fig.2.
2) Matlab plot for the algebraic expression (a) The frequency response of an LTI system is given by the transfer function evaluated on the unit circle
where For the first filter,
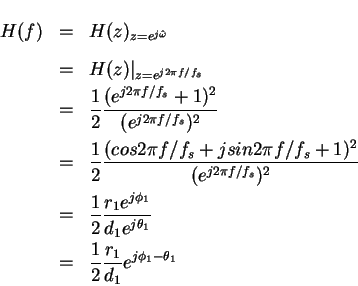
The magnitude response is
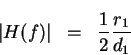
and phase response is
where
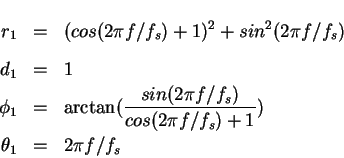
(b) For the second filter,
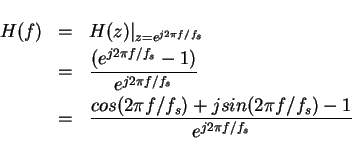
The magnitude response is and phase response is 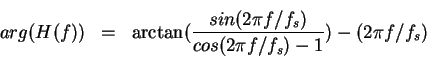
(c) For the third filter,
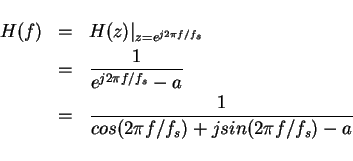
The magnitude response is 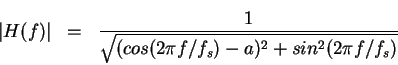
and phase response is 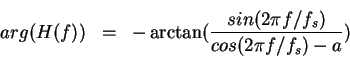
Magnitude responses and phase responses calculated from Matlab are shown in Fig.3 and Fi.4.
|