| F[z] | = | 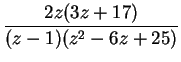 |
(12) |
2.1 Find the (causal) inverse z-transform of
| F[z] | = | 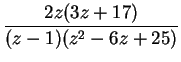 |
(12) |
using partial fractions.
2.2 Write numerical values for the coefficients of the first two tersm.
Solution.
2.1
The Eq.(13) can be expressed as a factored form
| F[z] | = | 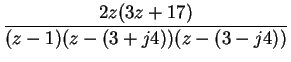 |
(13) |
First break F(z) into partial fractions
| = | 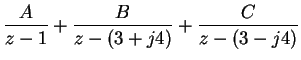 |
(14) |
| A | = | 2 | (15) |
| B | = | 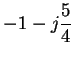 |
(16) |
| C | = | 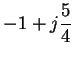 |
(17) |
| F[z] | = | 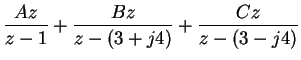 |
(18) |
![$\displaystyle \frac{cz}{z-p} \leftrightarrow cp^ku[k]$](img25.gif) |
(19) |
We take the inverse z-transform to obtain f[n]
| f[n] | = | Au[n] + B(3+j4)nu[n] + C(3-j4)nu[n] | (20) |
| = | ![$\displaystyle 2u[n] + (-1-j\frac{5}{4})(3+j4)^nu[n] + (-1+j\frac{5}{4})(3-j4)^nu[n]$](img26.gif) |
(21) |
2.2
The numerical values for the first two terms are
![\begin{eqnarray*}n = 0 & : & f[0]=0 \\
n = 1 & : & f[1]=6
\end{eqnarray*}](img27.gif)