Find
![]()
![]() [1 0 0 1]
[1 0 0 1]![]() and plot the magnitude and phase of Fr. Find the
and plot the magnitude and phase of Fr. Find the
![]() of Fr to verify it is equal to [1 0 0 1] as expected.
of Fr to verify it is equal to [1 0 0 1] as expected.
Solution.
The DFT of fk is
| Fr | = | 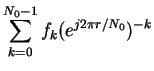 |
(17) |
| = | (18) | ||
| = | (19) |
| |Fr| | = | 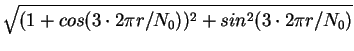 |
(20) |
| arg(Fr) | = | ![$\displaystyle arctan[\frac{-sin(3\cdot 2 \pi r/N_0)}{1+cos(3\cdot 2 \pi r/N_0)}]$](img30.gif) |
(21) |
The IDFT of Fr is
| fk | = | 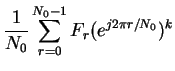 |
(22) |
| = | ![$\displaystyle \frac{1}{N_0}\sum_{ r= 0}^{ N_0 - 1 }[e^{-j2\pi r/N_0 \cdot 0} +
e^{-j2\pi r/N_0 \cdot 3}]e^{j2\pi rk/N_0}$](img33.gif) |
(23) |
Using
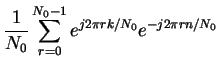 |
= | (24) |
where
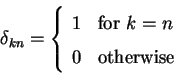
fk is
| fk | = | (25) | |
| = | (26) |