ELEC 200 - Engineering Graphics - Fall 2004

Transformations in the Euclidean Plane

>> % here is a simple function to demonstrate the effects of transforms by applying them
>> % to the unit grid (from -1 to +1 in x and y), and plotting the results


function pg(T, H)
  % -------------------------------------------------------------------
  % pg - Draw a unit grid from -1 to 1 in two dimensions.
  % Written by Bernie Till.  Last modified 29 Aug 2004.
  %
  % Call: pg(T, H)
  % Args: T - a transform to apply to the grid before plotting it
  %       H - a string to print as a heading
  % Rtns: none
  % -------------------------------------------------------------------

  v1 = [-1 -1; -1  1]; % vertical lines, endpoints as row vectors
  v2 = [ 0 -1;  0  1];
  v3 = [ 1 -1;  1  1];

  h1 = [-1 -1;  1 -1]; % horizontal lines, endpoints as row vectors
  h2 = [-1  0;  1  0];
  h3 = [-1  1;  1  1];

  v1 = v1 * T; v2 = v2 * T; v3 = v3 * T;
  h1 = h1 * T; h2 = h2 * T; h3 = h3 * T;

  axis([-3 3 -3 3], "square");
  if (nargin > 1) title(H); endif
  plot(
    v1(:,1),v1(:,2),"b", v2(:,1),v2(:,2),"k", v3(:,1),v3(:,2),"c",
    h1(:,1),h1(:,2),"r", h2(:,1),h2(:,2),"k", h3(:,1),h3(:,2),"m"
  );
endfunction


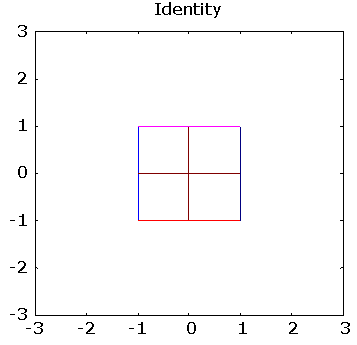
>> % lets start with the identity transform
>> pg([ 1  0;  0  1], "Identity")


          


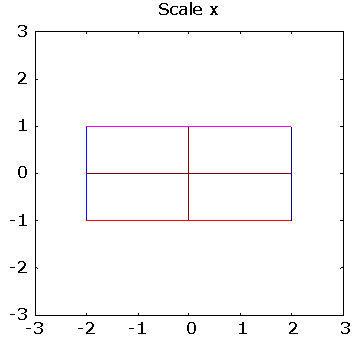
>> % scaling along the coordinate axes
>> pg([ 2  0;  0  1], "Scale x")


          


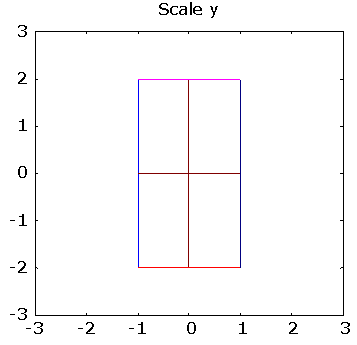
>> pg([ 1  0;  0  2], "Scale y")


          


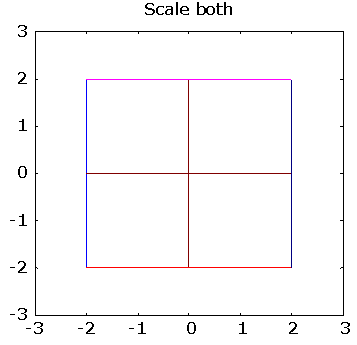
>> pg([ 2  0;  0  2], "Scale both")


          


>> % shearing along the coordinate axes
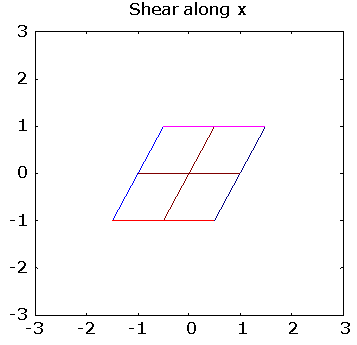
>> pg([ 1  0; .5  1], "Shear along x")


          


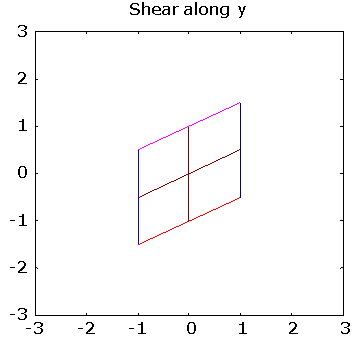
>> pg([ 1 .5;  0  1], "Shear along y")


          


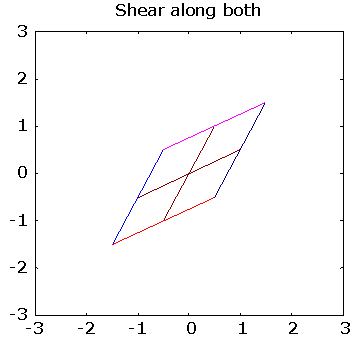
>> pg([ 1 .5; .5  1], "Shear along both")


          


>> % reflections across the coordinate axes
>> pg([-1  0;  0  1], "Reflection across x = 0")


          


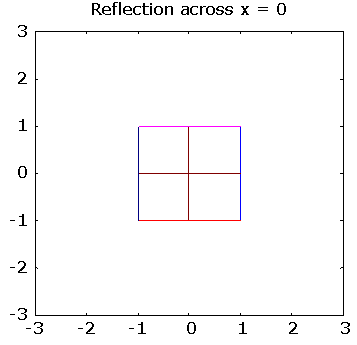
>> pg([ 1  0;  0 -1], "Reflection across y = 0")


          


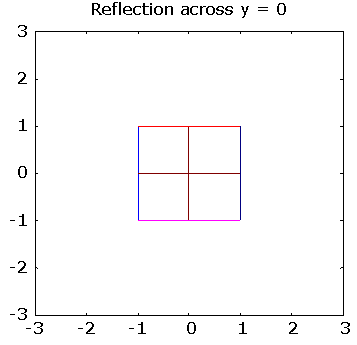
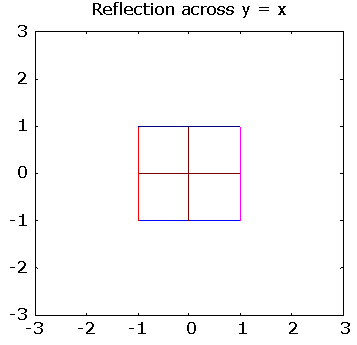
>> % reflections across + or - unit slopes
>> pg([ 0  1;  1  0], "Reflection across y = x")


          


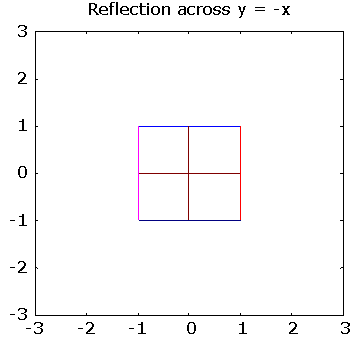
>> pg([ 0 -1; -1  0], "Reflection across y = -x")


          


>> % rotations
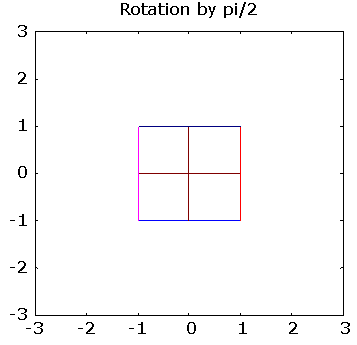
>> pg([ 0  1; -1  0], "Rotation by pi/2")


          


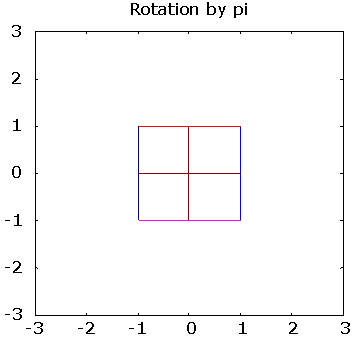
>> pg([ 0 -1;  0 -1], "Rotation by pi")


          


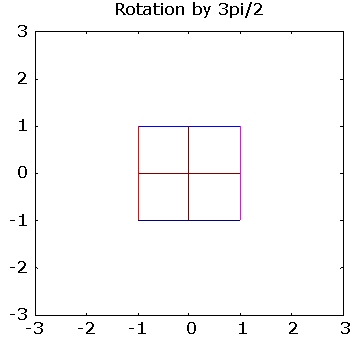
>> pg([ 0 -1;  1  0], "Rotation by 3pi/2")