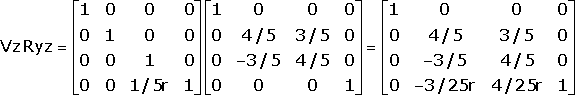ELEC 200 - Engineering Graphics - Fall 2004

Midterm Solutions

1. Show that a reflection across the yz plane, followed by a reflection across the zx plane, is equivalent to a rotation about the z axis.

   Let Fyz reflect across the yz plane and Fzx reflect across the zx plane. Then

   
   
   

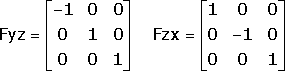
   The composition of these two reflections is just

   
   
   

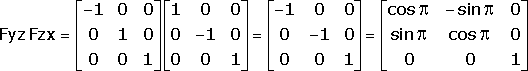
   Q.E.D.

2. Let Q be the matrix of endpoints of an arbitrary figure in space, let L be the matrix of endpoints of an arbitrary line in space, and let be an arbitrary angle. Write a MatLab function that rotates Q about L by and returns the result. Use 3D homogeneous coordinates.

   function Qbar = RotArbLine3D(Q, L, theta)
     d = L(:,2) - L(:,1); x = d(1); y = d(2); z = d(3);
     To = [ % translate the first point to the origin
        1    0    0  -L(1,1)
        0    1    0  -L(2,1)
        0    0    1  -L(3,1)
        0    0    0    1
     ];
     h = sqrt(y*y + z*z);
     Rx = [ % rotate about the x axis into the zx plane
        1    0    0    0
        0   z/h -y/h   0
        0   y/h  z/h   0 
        0    0    0    1
     ];
     r = sqrt(x*x + y*y + z*z);
     Ry = [ % rotate about the y axis into the z axis
       h/r   0  -x/r   0
        0    1    0    0
       x/r   0   h/r   0 
        0    0    0    1
     ];
     c = cos(theta); s = sin(theta);
     Rz = [ % rotate about the z axis by angle theta
        c   -s    0    0
        s    c    0    0 
        0    0    1    0
        0    0    0    1
     ];
     Qbar = inv(To) * inv(Rx) * inv(Ry) * Rz * Ry * Rx * To * Q;
   end
   

3. Let T(a, b, c) be the matrix that translates from the origin to point (a, b, c) and let S(s) be the matrix that scales by a factor of s in all 3 dimensions. Is it true that T(a, b, c) S(s) = S(s) T(a/s, b/s, c/s)? Prove your answer.

   Yes, they are equal. We have

   
   
   

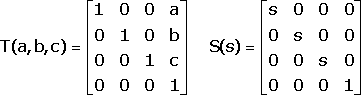
   thus

   
   
   

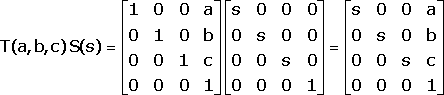
   and

   
   
   

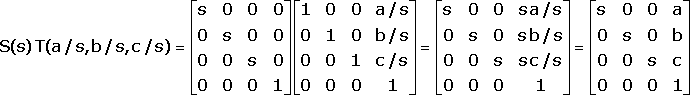
   Q.E.D.

4. Let Q be the matrix of endpoints of an arbitrary figure lying in the xy plane and let L be the matrix of endpoints of an arbitrary line lying in the xy plane. Write a MatLab function that reflects Q across L and returns the result. You may use 2D or 3D homogeneous coordinates.

   function Qbar = RefArbLine2D(Q, L)
     d = L(:,2) - L(:,1); x = d(1); y = d(2);
     To = [ % translate the first point to the origin
        1    0    0  -L(1,1)
        0    1    0  -L(2,1)
        0    0    1    0
        0    0    0    1
     ];
     h = sqrt(x*x + y*y);
     Rz = [ % rotate about the origin into the y axis
       y/h -x/h   0    0
       x/h  y/h   0    0 
        0    0    1    0
        0    0    0    1
     ];
     Fy = [ % reflect across the y axis
       -1    0    0    0
        0    1    0    0
        0    0    1    0
        0    0    0    1
     ];
     Qbar = inv(To) * inv(Rz) * Fy * Rz * To * Q;
   end
   

5. Derive the perspective transformation that looks at the origin from the point (0, 3r, -4r).

   The transformation we seek is obtained by rotating the viewpoint onto the z axis and applying a perspective transformation from the resulting point. Now, the distance of the point from the origin is

   
   
   

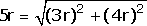
   so the matrix which rotates it onto the z axis is

   
   
   

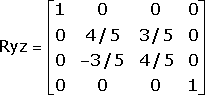
   After rotation, the point is located at (0, 0, -5r), from which point the perspective transform is

   
   
   

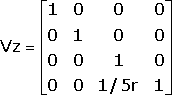
   Thus the effective transform is