Question 5
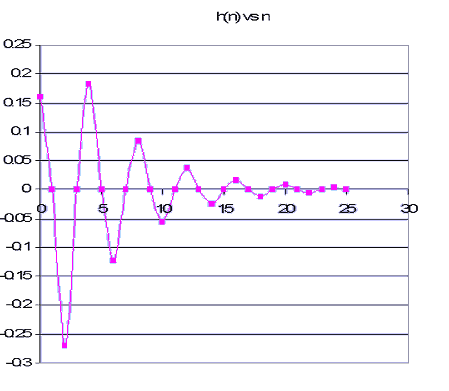
The impulse response h(n) was found using the difference equation obtained in question 3. Microsoft Excel was used to obtain numerical results for h(n), for n ranging from 0-25. The results are tabulated and graphed below.
N
|
x(n) |
y(n) = h(n) |
|
-2 |
0 |
0 |
|
-1 |
0 |
0 |
|
0 |
1 |
0.161 |
|
1 |
0 |
0 |
|
2 |
0 |
-0.26976 |
|
3 |
0 |
0 |
|
4 |
0 |
0.18222 |
|
5 |
0 |
0 |
|
6 |
0 |
-0.12309 |
|
7 |
0 |
0 |
|
8 |
0 |
0.083147 |
|
9 |
0 |
0 |
|
10 |
0 |
-0.05617 |
|
11 |
0 |
0 |
|
12 |
0 |
0.03794 |
|
13 |
0 |
0 |
|
14 |
0 |
-0.02563 |
|
15 |
0 |
0 |
|
16 |
0 |
0.017312 |
|
17 |
0 |
0 |
|
18 |
0 |
-0.01169 |
|
19 |
0 |
0 |
|
20 |
0 |
0.007899 |
|
21 |
0 |
0 |
|
22 |
0 |
-0.00534 |
|
23 |
0 |
0 |
|
24 |
0 |
0.003605 |
|
25 |
0 |
0 |
|
26 |
0 |
-0.00243 |

From the table and graph, it can be calculated that h(n) is less than 1% of its maximum value when n greater than or equal to 22.