1.1 For a transfer function with one pole and one zero, where (approximately) in the complex z-plane wolud you place the pole ![]() and zero z1 to obtain a high pass filter characteristic with zero response at f=0 and maximum response at f=fs/2 ?
and zero z1 to obtain a high pass filter characteristic with zero response at f=0 and maximum response at f=fs/2 ?
1.2 Draw a sketch to show the pole and zero locations.
1.3 Draw a sketch of the approximate frequency (magnitude) response.
1.4 Derive the diference equation to implement this high pass filter in terms of ![]() and z1.
and z1.
1.5 Draw a diagram of an impulse response of the filter.
Solution.
1.1
For a filter with one pole and one zero,
| H[z] | = | 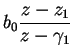 |
(1) |
| H(f) | = | (2) | |
| = | (3) | ||
| = | 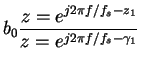 |
(4) | |
| = | 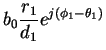 |
(5) |
where
| = | (6) | ||
| = | (7) |
Assume b0=1. From the table on the notes page 49, we can see that the pole ![]() should be located on the negative real axis, whereas the zero z1 on the positive real axis. If we leave the pole
should be located on the negative real axis, whereas the zero z1 on the positive real axis. If we leave the pole ![]() on the negative real axis within the unit circle and move the zero z1 to 1, H(f) becomes zero at f=0. For these z1 and
on the negative real axis within the unit circle and move the zero z1 to 1, H(f) becomes zero at f=0. For these z1 and ![]() ,
H(f) becomes maximum at f=fs/2.
,
H(f) becomes maximum at f=fs/2.
1.2
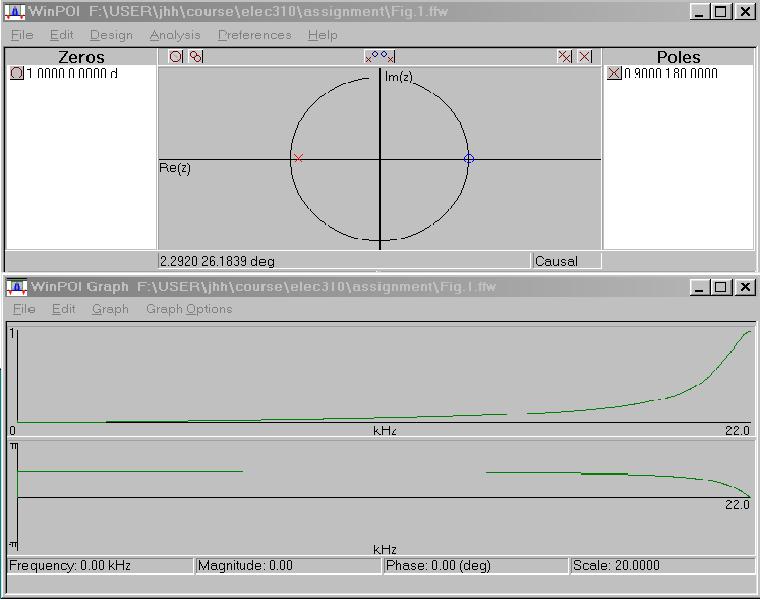
The pole and zero locations on the z-plane are shown in Fig.1(a).
1.3
Magnitude response of the H(f) is shown in Fig.1(b).
1.4
From H(z) in Eq.(1),
By applying inverse z-transform,
1.5 The block diagram of the filter is shown in Fig.2.
|