| = | ![$\displaystyle \sum_{ k= - \infty }^{ \infty } y[k]z^{-k}$](img29.gif) |
(23) | |
| = | ![$\displaystyle \sum_{ k= - \infty }^{ \infty } x[k-2]z^{-k}$](img30.gif) |
(24) | |
| = | z-2X(z) | (25) |
Design a simple digital filter whose trasnfer function corresponds to a delay of two sample times, i.e.
| y[k] | = | x[k-2] | (22) |
Assume a sampling frequency fs = 48 kHz.
3.1 Specify H(z).
3.2 Find the frequency response (amplitude and phase) of this filter.
3.3 Find the impulse response h[k] of this filter by taking the inverse z-transform of H(z).
3.4 Show by convolution that the output of the filter y[k] is x[k-2] as expected.
Solution.
3.1
Z-transform of y[k] is
| = | ![$\displaystyle \sum_{ k= - \infty }^{ \infty } y[k]z^{-k}$](img29.gif) |
(23) | |
| = | ![$\displaystyle \sum_{ k= - \infty }^{ \infty } x[k-2]z^{-k}$](img30.gif) |
(24) | |
| = | z-2X(z) | (25) |
Thus H(z) is
| H(z) = Y(z)/X(z) | = | (26) |
3.2
The frequency response H(f) is
| H(f) | = | (27) | |
| = | (28) | ||
| = | 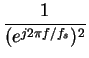 |
(29) | |
| = | 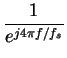 |
(30) | |
| = | 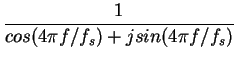 |
(31) | |
| = | 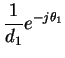 |
(32) |
The magnitude response is
| |H(f)| | = | (33) |
and phase response is
| arg(H(f)) | = | (34) |
| d1 | = | 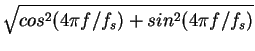 |
(35) |
| = | (36) |
3.3
From the z-transform pair
| (37) |
The impulse response of the filter is
| (38) |
3.4
Given filter impulse response h[k] and filter input sequence x[n], the filter out is
| y[k] | = | x[k]*h[k] | (39) |
| = | ![$\displaystyle \sum_{ n= 0 }^{ \infty }h[n]x[k-n]$](img43.gif) |
(40) | |
| = | ![$\displaystyle \sum_{ n= 0 }^{ \infty }\delta[n-2]x[k-n]$](img44.gif) |
(41) | |
| = | (42) | ||
| = | x[k-2] | (43) |